Math - Géométrie : Périmètre & Aire des Triangles

	evue	Théorie que vous devez savoir!
	apide

Mensuration - Formules pour le Périmètre et l'Aire (Surface) des Triangles

Le Périmètre d'une figure (plan) est la somme de ses côtés.
L'unité de périmètre est mètre (m) ou centimètre (cm).
L'Aire d'une figure (plan) est la surface enfermée par ses côtés.
L'unité d'aire est mètre carré (m²) ou centimètre carré (cm²).

Un triangle est un polygone qui a trois côtés.
Un triangle équilatéral a des côtés égaux et des angles égaux.
Un triangle isocèle a deux côtés égaux et deux angles égaux.
Un triangle scalène a trois côtés inégaux et trois angles inégaux.
Un triangle rectangle a un angle droit (90°).
Un triangle acutangle (triangle aigu) ou oxygone a tous les angles mesurant moins que 90°
Un triangle obtusangle (triangle obtus) ou ambligone a un angle mesurant plus de 90°.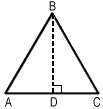

Périmètre d'un triangle = Somme de trois côtés
Dans la figure du ΔABC à côté, périmètre = AB + BC + AC.

Exemple
Calculer le périmètre (en cm) d'un triangle dont les côtés mesurent 10 cm, 20 cm et 30 cm.
Solution. cliquer ici pour la solution

Aire d'un triangle = ½ × Base × Hauteur
Tout côté du triangle mai être considéré comme sa base.
Alors, la longueur de la perpendiculaire du sommet opposé est considérée comme l'hauteur correspondante ou l'altitude.
Dans la figure du ΔABC à côté, aire = ½ × AC × BD.

Exemple
Calculer l'aire (en cm²) d'un triangle avec une base de 14 cm et une hauteur de 9 cm.
Solution. cliquer ici pour la solution

où a, b et c sont les longueurs des côtés du triangle,
et p = ½ (a + b + c) est le demi-périmètre du triangle.

Aire d'un triangle = √

p (p − a) (p − b) (p − c)

d'après la Formule d'Héron

Exemple
Les longueurs des côtés d'un triangle mesurent 3 cm, 4 cm et 5 cm. Calculer l'aire (en cm²) du triangle.
Solution. cliquer ici pour la solution

Aire d'un triangle équilatéral = √3 / 4 × Côté²
Dans le Δ ABC équilatéral, AB = BC = AC = a et AD = DC = ½ a a × √3 / 2 × a = √3 / 4 × a²

∴ En utilisant le Théorème de Pythagore, pour Δ ADB, hauteur = √

a² − (a / 2)²

= √3 / 2 × a

Aire = ½ × Base × Hauteur = ½ ×

Exemple
Si l'aire d'un triangle équilatéral est 16√3 cm², calculer son périmètre (en cm).
Solution. cliquer ici pour la solution

Dans le Δ ABC isocèle, AB = BC = a, AC = b

∴ En utilisant le Théorème de Pythagore, pour Δ ADB, hauteur = √

4a² − b²

/ 2

Aire = ½ × Base × Hauteur = ½ × b × √

4a² − b²

/ 2 = ¼ b √

4a² − b²

Aire d'un triangle isocèle = ¼ b √

4a² − b²

Exemple
Calculer l'aire (en m²) d'un triangle isocèle, dont chacun ses côtés mesure 10 m et sa base mesure12 m.
Solution. cliquer ici pour la solution

= ¼ (12) √

4 × 10² − 12²

= 48 m².

Aire d'un triangle isocèle = ¼ b √

4a² − b²

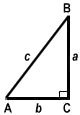
Aire d'un triangle rectangle = ½ × Produit des côtés contenant l'angle droit
Dans la figure à côté, Δ ABC est un triangle rectangle (ou un triangle à angle droit) ayant ∠ B = 90° dont l'aire = ½ ×AC × BC.
Noter que AB² = AC² + BC² (d'après le Théorème de Pythagore)

Exemple
La base d'un triangle rectangle mesure 3 cm et son hypoténuse mesure 5 cm. Calculer l'aire (en cm²) du triangle.
Solution. cliquer ici pour la solution

Dans le triangle rectangle Δ ABC, base AC = 3 cm et hypoténuse AB = 5 cm. ².

D'après le Théorème de Pythagore, hauteur BC = √

5² − 3²

= 4 cm.

Aire du triangle = ½ × AC × BC = ½ × 3 × 4 = 6 cm

Math - Géométrie Aide : Exercice de Pratique sur Périmètre & Aire de TrianglesMath - Géométrie Aide : Cours et Exercice sur Types de Triangles

Géométrie
& Aire des Triangles

Géométrie
& Aire des Rectangles et Carrés

12 more pages in Géométrie