Math - Géométrie : Périmètre & Aire des Quadrilatères II
Périmètre d'un rectangle = 2 (Longueur + Largeur)
Aire d'un rectangle = Longueur × Largeur Périmètre d'un carré = 4 × Côté Diagonale d'un carré = √2 Côté Aire d'un carré = Côté2 Aire d'un carré = ½ × Diagonale2 Aire d'un quadrilatère lorsque les diagonales se croisent aux angles droits = ½ × Produit des diagonales Aire d'un quadrilatère lorsque une diagonale et les longueurs des perpendiculaires de ses sommets opposés à cette diagonale sont données = ½ × Diagonale × Somme des longueurs des perpendiculaires Aire d'un parallélogramme = Base × Hauteur Aire d'un losange = ½ × Produit des diagonales Aire d'un trapèze = ½ × Somme des côtés parallèles × Distance entre côtés parallèles
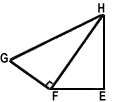
Exemple 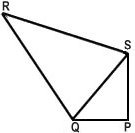
Exemple 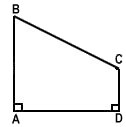
Example  Exemple La région ombrée de la figure donnée est une villa qui fait 68 m de long et 24 m de large. Elle est bordée par une pelouse d'une largeur uniforme de 6 m sur trois côtés. Calculer l'aire totale (en m2) occupée par la villa et la pelouse.
Solution.
L'aire totale occupée par la villa et la pelouse. = Longueur × Largeur
Math - Géométrie Aide : Exercice de Pratique sur Périmètre & Aire des Quadrilatères II
Lien lié de Math - Géométrie Leçons :
|
12 more pages in Géométrie

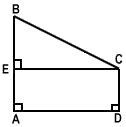 Puis, AE = 8 cm.
Puis, AE = 8 cm.