Math - Géométrie : Aire des Cylindres

evue Théorie que vous devez savoir ! apide

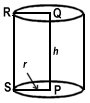
Aire (surface courbe) d'un cylindre = 2 π r h
où r est le rayon et h est la hauteur.
Dans la figure du cylindre à côté, r = PS = QR.
Dans la figure du cylindre à côté, h = PQ = RS.
Dans la figure du cylindre à côté, aire de la surface courbe = 2 π × PS × PQ.

Exemple
Calculer l'aire de la surface courbe (en cm²) d'un cylindre du diamètre de 14 cm et de la hauteur de 20 cm.
Solution. cliquer ici pour la solution

Aire (surface) totale d'un cylindre = 2 π r h + 2 π r²
Dans la figure du cylindre à côté, aire totale = 2 π × PS × PQ + 2 π × PS².

Exemple
Calculer l'aire totale (en cm²) d'un cylindre du rayon mesurant 3,5 cm et la hauteur de10 cm.
Solution. cliquer ici pour la solution

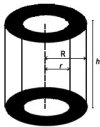
Aire (surface courbe) d'un cylindre creux = 2 π R h + 2 π r h
où R est le rayon externe et r est le rayon interne.

Exemple
Calculer l'aire de la surface courbe (en cm²) d'un cylindre du rayon externe mesurant 7 cm étant donné que son épaisseur est 1 cm et sa hauteur est 21 cm.
Solution. cliquer ici pour la solution

Aire totale (surface) d'un cylindre creux = 2 π R h + 2 π r h + 2 (π R² − π r²)

Exemple

Solution. cliquer ici pour la solution